2022を素因数分解するといくつ？
こんにちは。
中学受験コース算数科です。
来年は令和3年の西暦2021年。
算数科としてお届けする年の瀬の話題といえば西暦を扱った問題です。
今年もお届けします。
今年は2022年度入試で出題が予想される問題を多数用意してみました。
2021を素因数分解するといくつ？
令和3年は西暦2021年。
算数科としてお届けする年の話題は元号・西暦を使った問題です。
1.西暦2020年を素因数分解
東京オリンピックが開催された2021年ですが、大会名は東京2021ではなく、東京2020のままで行われました。
そんなことで、注目を浴びた1年の2021という数字に着目してみましょう。
梅干しを見ると唾液が出てくるのと同じように、算数科の人間は数字を見ると反射的に頭の中で素因数分解※してしまいます。
※素因数分解 正の整数を素数の積の形で表すこと
素因数分解をおこなえば、その数字が持つ性質を知ることができます。
2020は、2020＝2×2×5×101と分解できました。
したがって、2020は2や5や101の倍数であることが分かります。
2.2021を素因数分解する方法
まず、素因数分解をするときに、次のようなステップで検討を進めていきます。
➀素数を順に書き出してみる
→2 3 5 7 11 13 17 19 23 29 31 37 41 43 …
➁2から順に2021を割ってみる
2021÷3＝
2021÷5＝
2021÷7＝
2021÷11＝
‥‥‥‥‥‥‥‥
見つかりましたか？
順に割り算していき、割り切れた場合の商をさらに素因数分解していく。
そして、最後に素数が商になった時点で終了です。
素因数分解は、このような手順で進めていくしか方法はありません。
3.素数の発見法 エラトステネスのふるい
上記のように割り算していき、もし割り切ることができなければ、2021は「素数」となります。
※2021が素数であるかどうか、その結果は本記事の最後に記載します。
ここで素数かどうかを判定する場合、どの素数まで調査をすれば良いのか気になるところです。
そこで、次の「ふるい」という考え方を活用することになります。
エラトステネスのふるいと呼ばれる、素数を発見するために使われる方法です。
100以下の素数を、次のような方法で発見します。
2から100までの整数を書いてみます。
※1は素数ではないため、はじめから除外します。
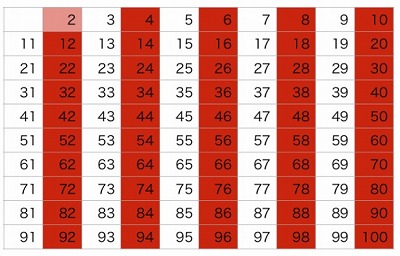
➀2を残し、2の倍数をふるい落とします
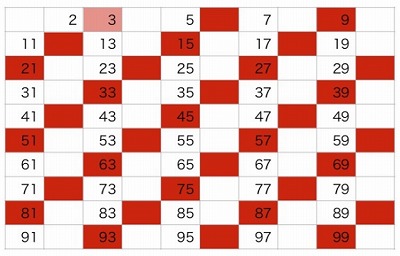
②3を残し、3の倍数をふるい落とします
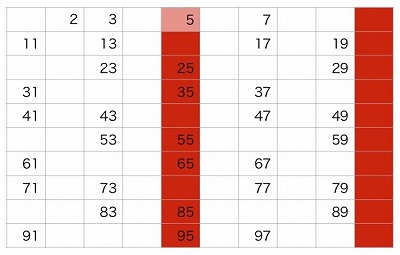
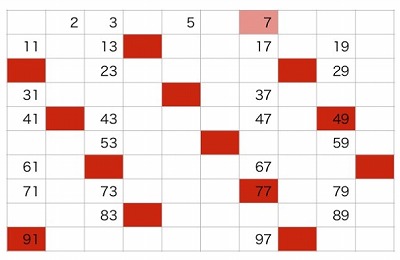
③5を残し、5の倍数をふるい落とします
④7を残し、7の倍数をふるい落とします
ここまでふるいに落とすことで、以下の整数が100以下の素数であることが分かります。
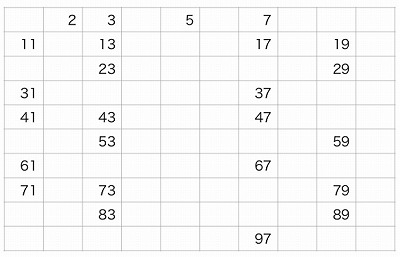
7の次の素数は11となります。
11の倍数は、11,22,33､…となりますが、
22=11×2 ←2の倍数で既にふるい落とされている
33=11×3 ←3の倍数で既にふるい落とされている
44=11×2×2 ←2の倍数で既にふるい落とされている
55=11×5 ←5の倍数で既にふるい落とされている
66=11×2×3 ←2の倍数で既にふるい落とされている
77=11×7 ←7の倍数で既にふるい落とされている
88=11×2×2×2 ←2の倍数で既にふるい落とされている
99=11×3×3 ←3の倍数で既にふるい落とされている
110=11×2×5 ←2の倍数で既にふるい落とされている
121=11×11 ←まだふるい落とされないでいる
したがって、7の倍数までふるいにかけることによって、121(11×11)未満の素数を発見できることができます。
4.2021の素因数分解の答え
エラトステネスのふるいの考え方を活用することで
「ある素数の倍数までをふるいにおとすことによって、その次の素数の平方数未満の素数を発見できる」ことが分かります。
よって、
47×47＝2209＞2021
を参考にすれば、43までの素数で割り切ることができなければ、2021は素数であることが確定します。
2021÷17＝
2021÷19＝
2021÷23＝
2021÷29＝
2021÷31＝
2021÷37＝
2021÷41＝
2021÷43＝47
割り切れた!!!
43で割り切れなければ、素数確定でしたが、最後の最後で大逆転勝利!!!
(感動的!!!)
2021は素数ではなく、43と47の倍数であることが判明しました。
5.2021のまとめ
算数では、西暦・元号に関連する問題が出題されることがあります。
受験生は、2021＝43×47であることは事前に知っておいた方がよさそうです。
中学受験コースでは、西暦・元号に関連する予想問題を作成していきます。
最後までおつき合いいただき、ありがとうございます。
みなさま良いお年をお迎えください。
国大Qゼミ中学受験コース 教務責任者
