受験対策ブログ
カレンダーで学ぶ!中学受験算数

算数であつかう大切な視点の宝庫
こんにちは。
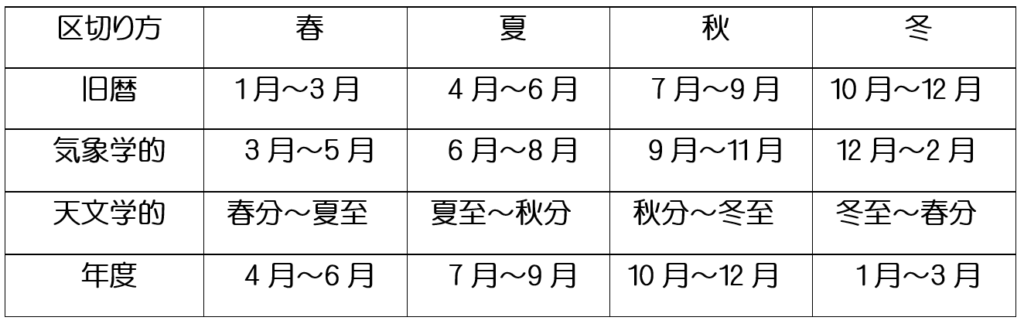
先日、5年生の授業内で、ある子どもが「最近は春と秋を感じる期間が短い気がする」と発言していました。
毎年5月頃から9月頃まで気温が高い日が続くという意図での発言でしたが、その後、自然に四季の区切り方について話題になりました。
タブレットを使った授業をしていると大変便利なものです。
四季について検索をし、子どもたちと共有しました。
カレンダー算(日暦算)
算数で季節(暦)に関する問題といえば、カレンダー算(日暦算)があります。
日数の計算をしたり、曜日を求めたりする問題です。
例えば
(フェリス女学院中学)
カレンダーは、算数であつかう大切な視点が数多く含まれています。
ここに9月のカレンダーがあります。
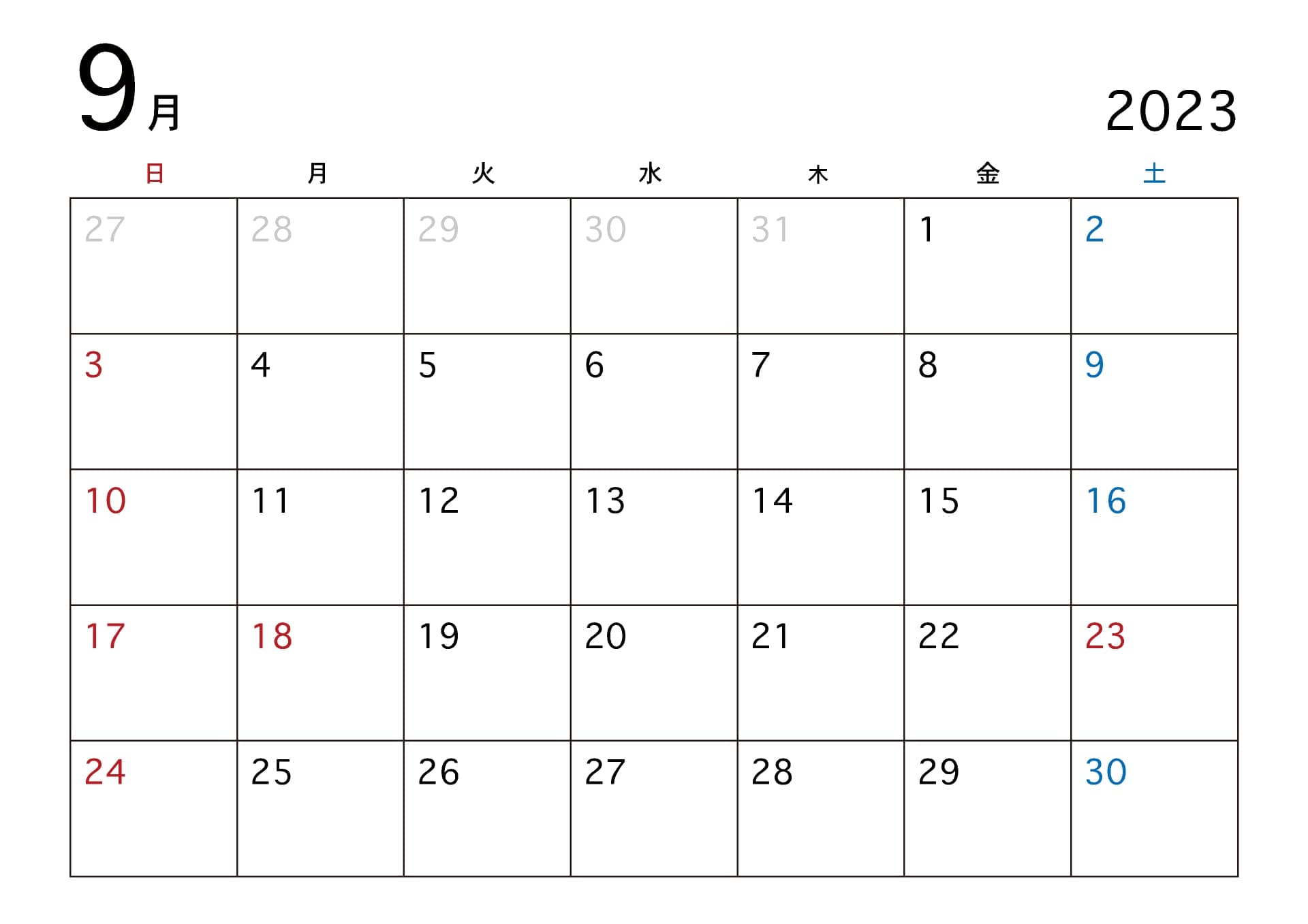
・タテで見ると7ずつ増える
・6日を起点に左ななめ下に6の段が続くなど
→周期算 等差数列
土日は5週あるが他は4週
→規則性(他の月のカレンダーは「4週曜日」と「5週曜日」がどうなっている!?)
金曜日は7の倍数 月曜日は7でわると3あまる
→余りによる分類(数の性質)
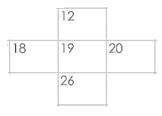
カレンダーの場合、中央の数字が5つの数の平均値になる性質があるので、図の場合、5つの数字の和は、19が平均なので19×5=95
→文章題(平均 和差算 分配算)
また、年間カレンダーを見ると、次のような面白い特徴があります。
→2023年は、全て金曜日です。
→2023年は、全て火曜日です。
※これらは、各日付の間が7の倍数(すべて63)になっているために起こる現象です。
カレンダーから作問をするだけで、簡単に算数に触れることができます。
入試問題にもどります。
一般的な解き方は、次の通りです。
4月→30日
5月→31日
6月→30日
7月→7日
30+30+31+30+7=128日
3/1の128日後が7/7となる。
128÷7=
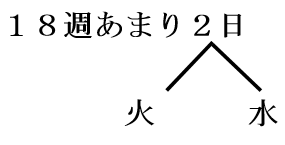
3/3と5/5と7/7が同じ曜日となることを知っている受験生は数多くいます。
その場合には、3/3が水曜日であることを求めて、そこから7/7も水曜日であることを計算などせずに求めることになるでしょう。
中学入試で出題される問題は、どこの学校でも練りに練った傑作が登場することが多いのですが、このように知識重視の日付設定にした意図が何であるのか、作問した先生に聞いてみたくなりますね。
https://www.qzemi.com/category/school/junior/20230619


