受験対策ブログ
【中学受験】「2026」に絡めた出題予想!

年末恒例「2026」を使った入試予想問題に挑戦!
今年も年の瀬の話題として中学入試に出題が予想される「西暦」問題をお届けします。
各問題の正解は本稿の最後に記載しています。
初級問題
📝西暦2026年の各位の数に着目した問題
■問題1
2026は「0」と「2」と「2」と「6」を使って表すことができる数字です。
「2026」のように「0」を1個、「2」を2個、「6」を1個使ってできる4けたの整数は何個ありますか。
📝素因数分解の問題
■問題2
2026を素因数分解しなさい。また、2026の約数は何個ですか。
「2026の約数」は何個あると思いますか。予想してみてください。
- ① 4個
- ② 10個
- ③ 18個
- ④ 30個
素因数分解とは「正の整数を素数の積の形で表す」ことを言います。
2026を素因数分解するとどうなるでしょうか。
素因数分解をするときに、次のようなステップで検討を進めていきます。
- 素数を順に書き出してみる。
→2 3 5 7 11 13 17… - 2から順に2026を割ってみる。
- 順に割り算していき、割り切れた場合の商をさらに素因数分解していく。そして、最後に商が素数になった時点で終了です。
さて、2026でやってみると…
2026÷2=1013
※1013は素数なのでこれで終わり。つまり2026を素因数分解すると 2×1013。
2026=2×1013なので、約数は
1、2、1013、2026 の4個
(①が正解)です。
大きな数字の割には個数が少ないですね。
中級問題
📝約数の数の問題
■問題3
2026の約数は、1、2、1013、2026 の4個あります。約数が4個となる小さい方から10番目の整数はいくつですか。
これは問題2の逆思考問題で、約数の個数から整数を求める問題です。
小さい方から「10番目」の数を求めるのであれば、地道に調査していく方法で良いと思います。
参考までに、受験算数では以下のように論理的に調べる方法もあります。
約数が4個となる整数は、次の①、②のいずれか。
② □1×△1
○、□、△ともに素数
①の場合
○=2のとき、23=8
○=3のとき、33=27
○=4のとき、43=64
…
②の場合
次のように表にしてみる。
横が□に入る数字、縦が△に入る数字として、それぞれの積を記入する。
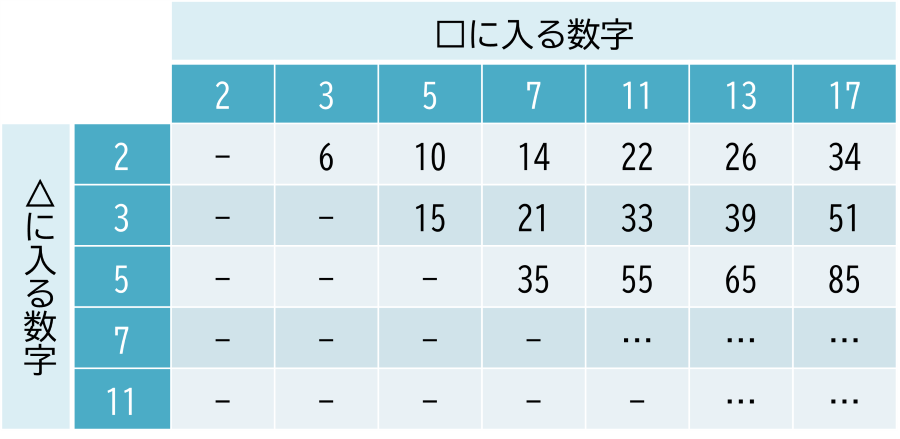
①、②の結果を合わせて、小さい方から順に書き出すと、
6、8、10、14、15、21、22、26、27、33、・・・
であるため、10番目は33 となる。
定番の問題
算数の単元名の中で「周期算」というものがあります。あるきまりで数字や記号が並べられていて、そのN番目が何であるのかを調べたり、N番目までの数字の和を求めたりする問題です。
次の問題は、数字が「2026」になることで特別な技術が必要になるわけではありませんが、小問系の問題の中で出題が予想されます。
📝周期算の問題
■問題4
2×2×2のように2を3回かけた数の一の位は8です。2を2026回かけた数の一の位はいくつになりますか。
を小数で表したとき、小数第2026位の数はいくつですか。
2026チャレンジ問題
その他、「2026」が関係する問題として最後に2問紹介します。
📝西暦と年令の問題
たかし君の誕生日は2013年6月2日で、2026年2月1日現在で12歳です。誕生日である6月2日を基準に考えると、「西暦」と「たかし君の年令」の関係は次のようになります。
なお、年令は「数え年(生まれた瞬間から1歳と数え始める)」ではなく、「満年齢(生まれた時を0歳として誕生日ごとに1歳ずつ増える数え方)」を使用します。

- (1) 上の表で、「西暦の年号」を「たかし君の年令」で割る計算をします。たかし君が1歳から4歳までの中で、この割り算の結果が割り切れるのは、たかし君が何歳のときですか。すべて求めなさい。ただし、整数計算で「割り切れる」とは、商が整数になることを表します。
- (2) たかし君の年令が5歳以上の場合も(1)と同じ割り算をしていきます。割り算の結果が割り切れるときのたかし君の年令を(1)の答えを含めてすべて求めなさい。
ただし、答えは100以下とします。
問題6は「2026」であるからこそ出題されるというわけではありませんが、他の問題でも使える汎用性の高い解法を含んでいます。
「西暦」と「たかし君の年令」の関係に着目します。西暦が1つ大きくなれば、たかし君の年令も1歳増えるので、「西暦」と「たかし君の年令」の差は常に2013で一定となります。これをもとにして、「西暦の年号」÷「たかし君の年令」が割り切れるためには、たかし君の年令が2013の約数となる必要があります。よって、2013を素因数分解してみると良いですね。
📝各位の和が同じ数の問題
■問題7
2026は、各位の数の和が 2+0+2+6=10 となります。各位の数の和が10となる整数を並べたとき、2026は小さい方から何番目ですか。
問題7は少し難易度が高いですが、各位の数の和がキリのよい「10」になる問題なので、算数的には面白い問題と言えるでしょう。
参考までに、解き方の一例を記します。
まず、3桁以下の整数をについて考える。
次の図のように、ボール10個と仕切り2本を準備する。
○○○○○○○○○○//
例えば、○○/○○○○○/○○○は 253 を表し、各位の数の和は 2+5+3=10 となる。同じく、/○○○○/○○○○○○は 46を表し、各位の数の和は4+6=10となる。
ボール10個と仕切り2本の並べ方は
66通り
ただし、
○○○○○○○○○○//
/○○○○○○○○○○/
//○○○○○○○○○○
の3通りは整数にならないため除く(1つの位に「10」を入れることはできないため)。
したがって、3桁以下の整数は 66−3=63通り
次に、4桁で千の位が1の場合を考える。
次の図のように、ボール10個と仕切り3本を準備する。
○○○○○○○○○○///
千の位は1なので、仕切りのうちの1本は次のように固定する。
○/○○○○○○○○○//
固定していない部分(○○○○○○○○○//)の並び方を考えればよいので、
ボール9個と仕切り2本の並べ方は
55通り
したがって、千の位が1の整数は 55通り
千の位が2の整数は、2008、2017、2026の3通りなので、ここまで求めた3桁以下の整数と4桁の整数の数の和を求めると
63+55+3=121
2026は121番目となる。
さいごに
受験算数では、西暦に関連する問題が出題されることがあります。今回は、その一部をご紹介しました。
受験生は「2026=2×1013 (1013が素数であること)」を知っておいた方が良さそうです。また、「2027」「2029」は素数となるため、来年以降の入試では、素数に関する出題が増えるのではないかと予想しています。
最後までお付き合いいただき、ありがとうございます。
みなさま、良いお年をお迎えください。
★問題の解答★
問題1 9個
問題2 2×1013、4個
問題3 33
問題4 4
問題5 2
問題6 (1)1歳、3歳
(2)1歳、3歳、11歳、33歳、61歳
問題7 121番目


